Quick Guide to Optimization of Algorithms
Learn the time complexity concepts in an easy way!
If you liked this article, please share it with your friends too!
After making a friend understand these concepts, I decided to write an article to bring an end to the unending requests by my friends to teach this topic.
Disclaimer: I have to do some trade-offs to reduce the complexity and make it simple for general readers to understand the concept. So, If you are a computer scientist who will sue me in the local court for scientific inaccuracies probably this blog is not for you :(
What is Optimization?
Optimization means making the algorithm in such a way that it takes less time than earlier. This may involve eliminating redundant lines of code that do no good but result in more time taking.
Suppose I asked you to guess a number from 1 to 15 that I have selected and there is no limit to the number of guesses that you can make:
(i) Linear Search: You can guess all the way from 1 to 9 taking 9 steps in solving the problem.

(ii) Binary Search: You can guess smartly by picking only the center elements and at max, it will take just 4 steps!

How do I know which algorithm is the best
Okay, Now I agree that we always have a better solution to every problem. But how do I know which solution is better than the rest of the others?
Simple answer! That could be done by looking at the piece of code you have written. Let's say we have this code to find if a number is prime or not:
#include <stdio.h>
int main() { // 1 u
int num = 11677, i = 2; // 1 u
for (i = 2; i < num; i++) { // n u
if (num % i == 0) { // 1 u
printf("Not Prime Number\n"); // 1 u
return 0; // 1 u
}
}
printf("Prime Number\n"); // 1 u
return 0; // 1 u
}
This algorithm took 11766 iterations to find out if 11677 is prime number or not!
If each step is associated with a cost let's say unit of time on the basis of its repetition.
Total cost will be = (7 + n) and its time complexity is O(n)
Now you are assigned the task to optimize this algorithm so it takes less time to execute. You are smart so instead of dividing the num with each value of 'i', you took the square root of num and run the loop only that many times.
#include <stdio.h>
int main() { // 1 u
int num = 11676, i = 2; // 1 u
while ( i * i <= num) { // log(n) u
if (num % i == 0) { // 1 u
printf("Not Prime Number\n"); // 1 u
return 0; // 1 u
} else { // 1 u
i++; // 1 u
}
}
printf("Prime Number\n"); // 1 u
return 0; // 1 u
}
It took 108 iterations to find out 11677 is a prime number.
I need to do the maths again, we calculate the total cost by assigning unit of cost to each step on the basis of repetitions.
Total Cost is equal to = (9 + log (n)) and its time complexity is O (log (n))
Now, we know 2nd algorithm is much more efficient than the first one. But how?
Isn't it true that log(n) < n ?
Example: log (8) = 3 and obviously 3 < 8
This is how we get to know one algorithm is better than the other.
Rules to Calculate Time Complexity
Hmm... But I noticed something! Why we are ignoring constants like I said time complexity is O (log n) not O (4 + log n)
The reason for this suppose we have this:
int a = 5;
This statement will take a fixed time and the size of the input will not affect this statement. Therefore, we ignore it completely.
Oh! Hmm... Is there another rule that we should abide by?
Yes, There are 2 more essential rules that should be followed for quick estimation:
If there is any coefficient of the 'n' then it must be eliminated.
For example, there is a program with 2 loops in it therefore the time complexity is:
Suppose Time Complexity = O (n + n) = O (2n)
But the coefficient must be eliminated thus T.C. becomes O (n)
Only the 'n' with the highest power should remain and eliminate others.
For example, a program has two kinds of loops: a nested loop and a simple loop.
Suppose Time Complexity = O (n * n + n) = O (n^2 + n)
But only the highest power of 'n' should remain so:
Time Complexity = O (n^2)
What are Asymptotic Notations?
This brings us to the new topic asymptotic notations. The term can be broken down into two terms:
(i) Asymptote: A line that is approached by a curve but never gets intersected. The distance between the curve and asymptote approaches zero.
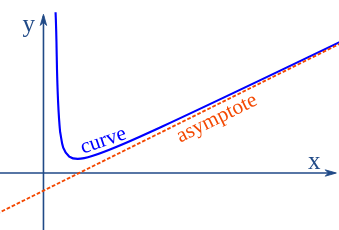
Image Source: mathsisfun.com
(ii) Notation: A symbol used to denote a value or information.
To understand asymptotic notations we need to learn about bounds.
Bound -> A kind of limit that cannot be crossed
Upper Bound is the maximum limit of anything that can be achieved.
Lower Bound is the minimum limit of anything that can be achieved.
How much time an algorithm is going to take depends upon the size of the input.
The greater the input, the more time it takes
Let's again take the easy example of a prime number algorithm.
You remember it was taking at max log (n) iterations to find out if a number is prime or not.
Below is a table that tells how many iterations will the algorithm takes for larger numbers.
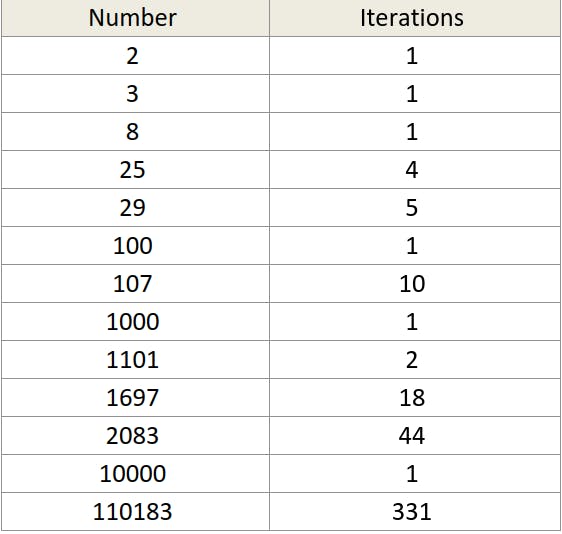
But you said that number of repetitions will be log (n) where n is the number. Then why even for big numbers like 10000 it is taking just 1 repetition?!
I said that AT MAX it will take log (n) repetitions as it is in the case of 2083. It is not necessary that all the numbers will take log (n) repetitions.
If we plot the graph of Maximum Iterations on a cartesian plane. It will look like this:
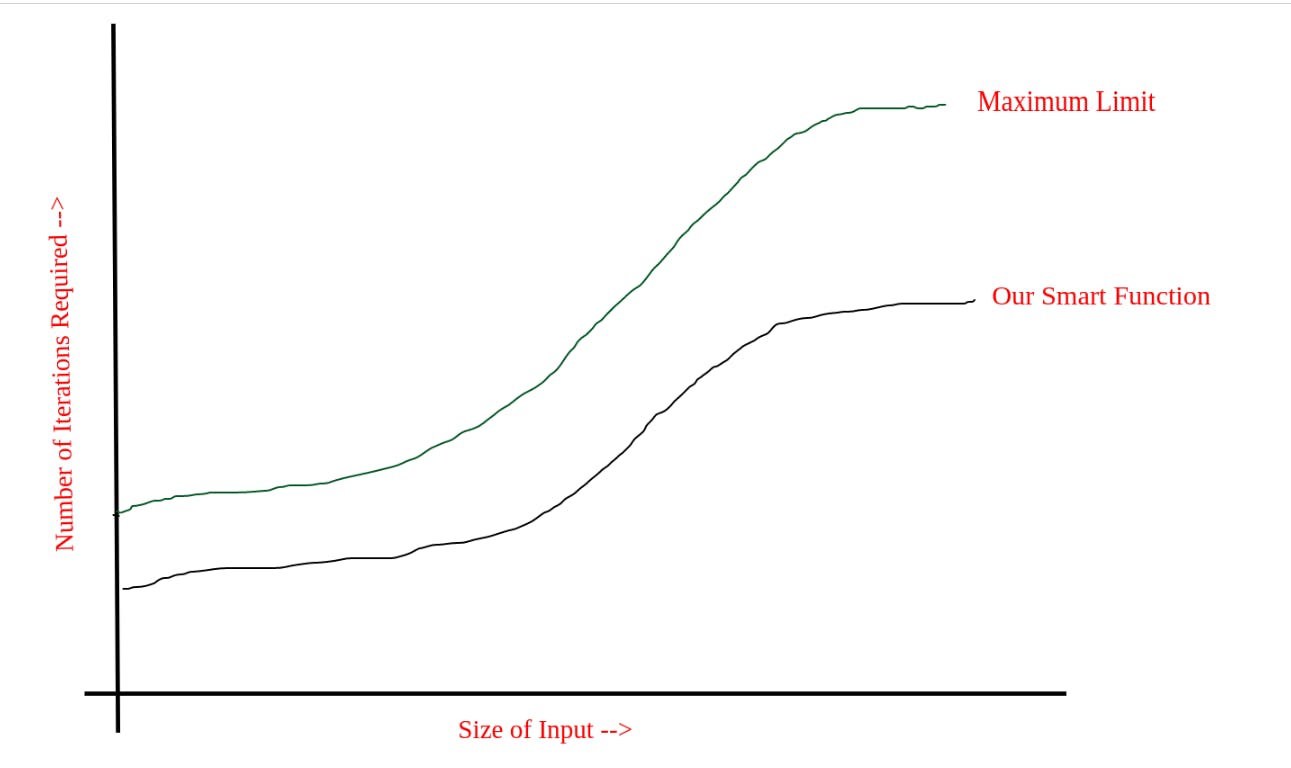
And look how our smart function is taking way too less iterations than the maximum repetitions allowed.
Similarly, we observed that the program is running at least once. Therefore, we get to know that there are minimum iterations as well for each program.
If we plot the Minimum Limit graph along with the Maximum Limit graph we get something like this:
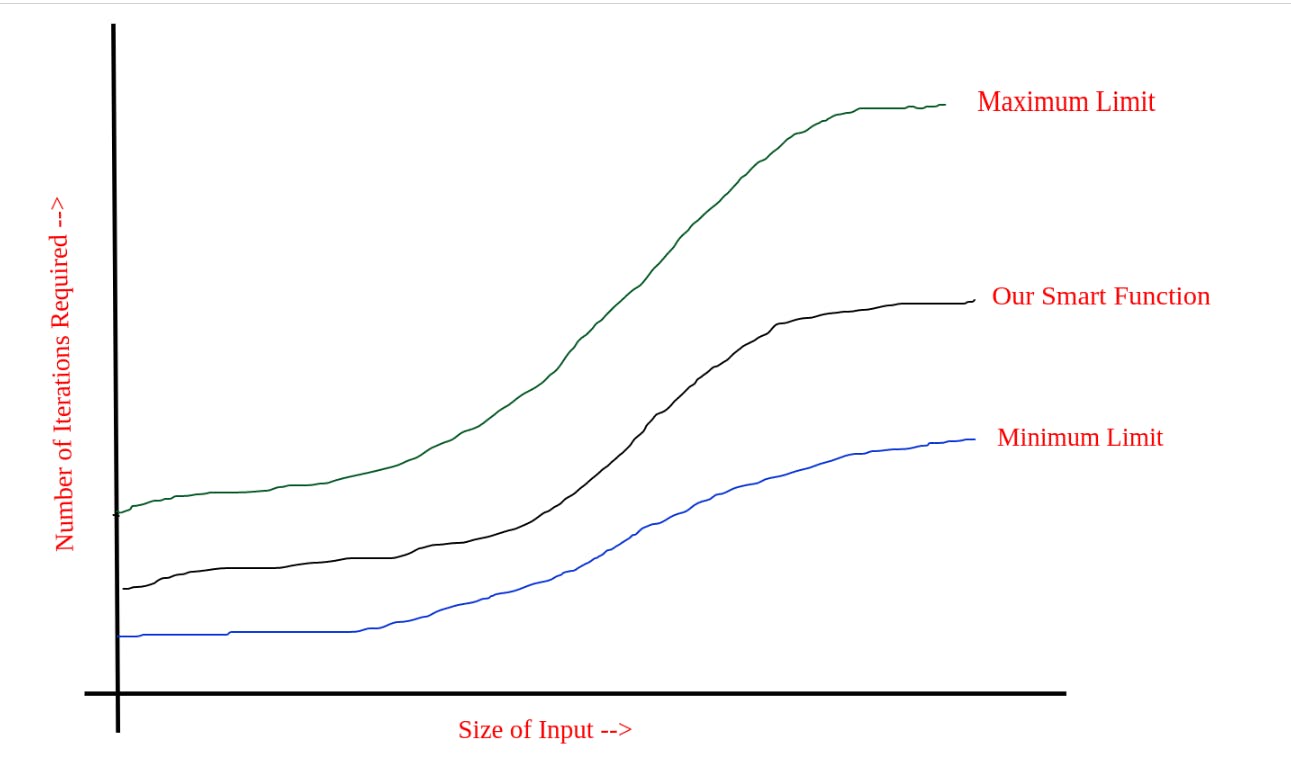
Wallah! This is a beautiful graph, isn't it?
The maximum limit of f (x) is the upper bound and the minimum limit of f (x) is the lower bound. So we get to know that asymptotic notations are nothing but a fancy term for different bounds.
Big Oh ('O') : tells us the upper bound of the function
Big Omega ('Ω') : tells us the lower bound of the function
Big Theta ('θ') : tells us both the upper and lower bounds
Efficiency cases and comparison
Do you know that the same algorithm can execute blazingly fast and sluggishly slow in different scenarios?
Surprised? Here is why:
Suppose you are searching for an item in a grocery list of 100 items. There are three cases of how you find your item:
Case 1: It is possible the item you are searching for is at the very top of the list. So, it will take you just one step.
Case 2: It is possible that the item is somewhere in the middle of the list. Let's say it took you 43 steps.
Case 3: Or it is possible that the item is the last item or it is not on the list.
Assume that the item was at the top so it took just one step for you. Can we conclude that this is the best way of solving this problem?
Or say the item was at the end of the list. Can we conclude that this algorithm is the worst way of solving this problem?
Of course not! These are different cases that tell about the efficiency of the algorithm in varying situations.
Case 1: Getting the item in one step is the 'Best Case'
Case 2: Getting the item at the end of the item that is not on the list is the 'Worst Case'
Case 3: Getting the item somewhere in the middle of the list is 'Average Case'
As I have said one algorithm can be good or bad depending on the problem it is solving and the size of the input.
Here below is the graph that tells us what time complexity is better than others:
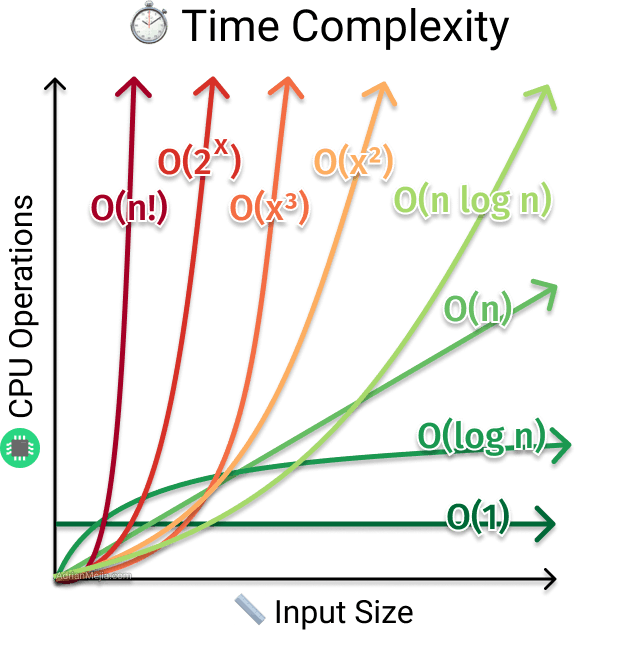
Image Source: adrianmejia.com
Further Readings
Okay, that's it for today! Hope you guys liked it and please share it with your friends.
